AI-02 Problem Solving in AI

AI Problem

• A problem in AI is a task or situation where a computer or machine needs to think, decide, or learn in order to solve something intelligently

• A problem in AI is defined by: Inputs, a goal, and a way to reach that goal using logic, rules, or learning.

• Example:

  • Problem: A self-driving car reaching a destination safely.
  • Inputs: Current location, Map data, Traffic signals, Nearby vehicles, Weather conditions
  • Goal: Reach the destination safely, quickly, and without breaking any traffic rules.
  • Way to reach the goal: Use AI to analyze surroundings, make decisions (like when to stop or turn), and learn from past drives to improve navigation.

• AI problem components:

  • Initial State – Starting point
  • Goal State – What we want to achieve
  • Actions – What can be done
  • Transition Model – What happens when actions are taken
  • Path Cost (optional) – How much each step costs (used in optimization)

• Real-life examples:

  • Diagnosing diseases from symptoms
  • Translating languages (e.g., Google Translate)
  • Recommending movies (e.g., Netflix)
  • Detecting banking fraud

Problem Type	Description	Example
Search problem	Find the best solution from many options .	GPS finding the shortest route
Planning problems	Decide steps to reach a goal.	Robot making tea
Classification	Group data into categories.	Spam or Not Spam emails
Prediction	Guess future results from past data.	Weather forecasting
Decision making	Pick the best option from choices.	Chess AI choosing next move
Perception	Understand inputs like images, sounds.	Face recognition, self-driving
Learning problems	Learn from past experience to improve.	Machine learning model training

What does it mean to define AI Problem

• In Artificial Intelligence, before solving a problem, we need to clearly define it — just like we need to understand the rules before playing a game

• We define:

  • Where we are (Initial State)
  • Where we want to go (Goal State)
  • What we can do (Possible Actions / Rules)

• Example-1: Taxi Booking App (AI finding the best route)

  • Initial State: Your current location
  • Goal State: Your destination
  • Actions: Choose among different routes, avoid traffic, follow navigation rules

• Example-2: Cooking Assistant AI

  • Initial State: Ingredients you have
  • Goal State: Desired dish (e.g., pasta)
  • Actions: Mix, boil, chop – in correct sequence

• Example-3: Washing Clothes with AI Washing Machine

  • Initial State: Dirty clothes in the basket
  • Goal State: Clean, dry clothes
  • Actions: Fill water, add detergent, wash, rinse, dry

---

Problem Space & State Space

• In AI, before solving any problem, we must clearly define what the problem is and how to approach it — that’s where problem space and state space come in.
• Problem space and state space help AI understand: "Where can I go, what can I do, and how do I get to my goal efficiently?"

State Space

• All possible situations (states) the system can be in while solving the problem
• It includes:
  • The initial state
  • The goal state
  • All intermediate states you can reach by applying different actions

Problem Space

• Problem Space = The combination of: State Space + All possible actions (rules or moves that change one state to another)
• Problem Space = State Space + Actions
• It defines the entire environment in which the AI must operate to reach a goal.
• It defines all possible steps AI can use to reach the goal

Example

• Making a burger: AI as a cooking assistant
  • Imagine you're teaching a robot (AI) how to make a burger.
  • Problem space = Every action AI can take (adding patty, adding cheese etc)
  • State space = Every stage in burger-making
  • Goal = Perfect burger

---

Search Strategies

• Search strategies help an AI find the path from the starting point to the goal, especially when the AI has many choices to make.
• Imagine AI is playing a maze game, and it needs to find the quickest way out.
• Search strategies guide how it explores the maze.
• Two main types:
  • Informed Search
  • Uninformed Search

Informed	Uninformed
Search with extra information	Search without an information
Uses knowledge to guide steps	No prior knowledge
Finds solution quickly	Slower & time-consuming
Less complex (Time + Space)	More complex (Time + Space)
Uses: DFS and BFS	Uses A*, Heuristic DFS,

• References:
  • Informed Search
  • Uninformed Search

---

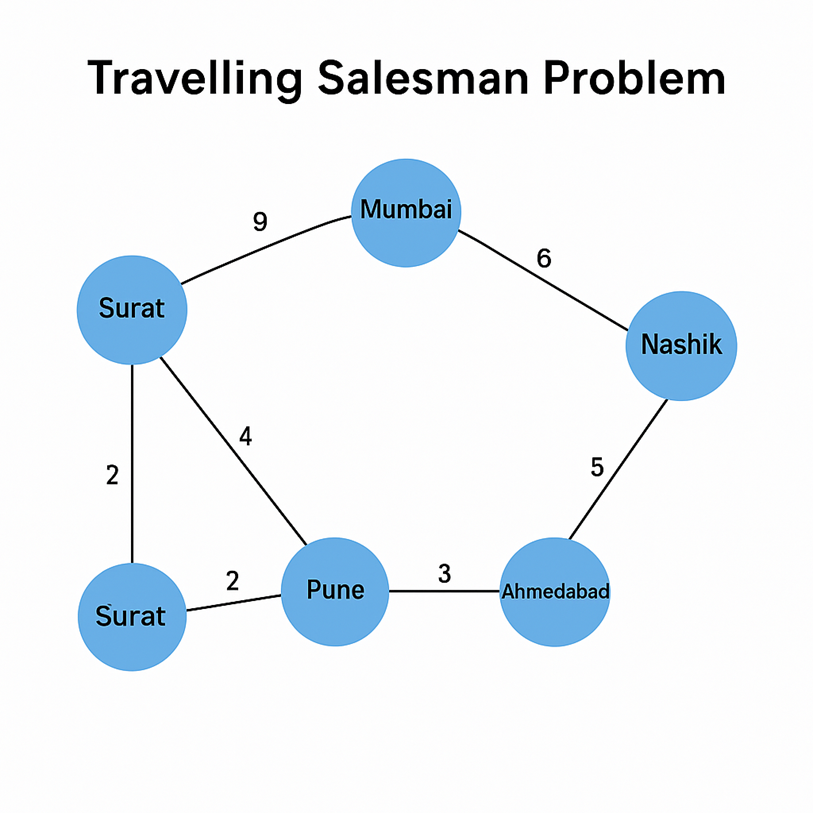
Travelling Salesman Problem

• Given a list of cities and the distances between each pair, what is the shortest possible route that:

  • Visits each city exactly once, and
  • Returns to the starting city

• Example: A salesman needs to visit 5 cities: Surat → Mumbai → Pune → Nashik → Ahmedabad

• Goal:

  • Visit each city once
  • Travel the least distance (or time/cost)
  • Return to the starting city

• Uninformed Search (Brute Force):

  • Tries every possible route
  • For n cities, number of possible paths = (n − 1)!
  • For 5 cities: (5 − 1)! = 24 possible paths
  • Guaranteed to find optimal solution
  • But not scalable — what if 99 cities?

• Informed Search (Heuristics):

  • Uses smart logic or heuristics
  • Doesn’t check every path
  • Much faster and more efficient

---

Breadth First Search (BFS)

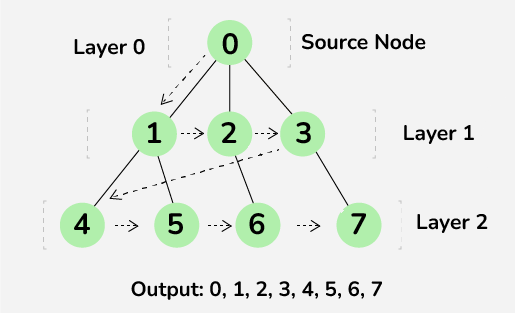
• BFS is a traversal approach in which we first walk through all nodes on the same level (horizontal movement) before moving on to the next level.
• BFS visits siblings before children
• BFS uses Queue data structure for finding the shortest path.
• It works on the concept of FIFO (First In First Out).
• BFS is more suitable for searching vertices closer to the given source.
• In BFS, each node is traversed only once.
• BFS will definitely find a solution if it exists
• BFS uses more memory than DFS
• How it works:
  • Start from the root/start node
  • Visit all its immediate neighbours
  • Then go to next level of their neighbours
  • Keep repeating until goal is found or all nodes are visited
• Real-life example:
  • Social Media Friend Suggestions: Starting from you, BFS checks all your direct friends (level 1). Then their friends (level 2), and so on.
  • Web Crawlers: Search engines like Google crawl the web page level by level. First links on page → then links inside those links
• Use cases:
  • Shortest path in maps (like Google Maps)
  • Puzzle solvers (like 8-puzzle, word ladder)
  • Web Crawling
  • Social networks – friend suggestion

---

Depth First Search (DFS)

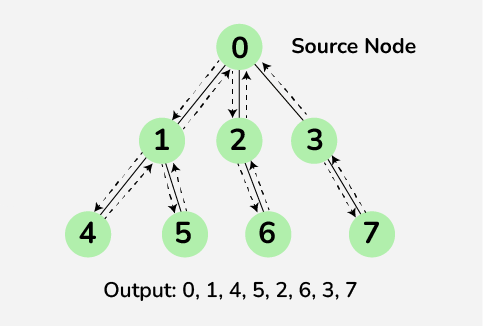
• DFS is a traversal approach in which the traverse begins at the root node and proceeds through the nodes as far as possible until we reach the node with no unvisited nearby nodes
• DFS visits children before siblings
• DFS uses Stack data structure.
• It works on the concept of LIFO (Last In First Out).
• DFS is more suitable when there are solutions away from source.
• In DFS each node is traversed twice due to backtracking.
• DFS may lead to situations where the algorithm gets stuck in an infinite loop.
• DSF may not give shortest path
• The amount of memory required for DFS is less than that of BFS.
• How it works:
  • Start from the root/start node
  • Visit one child node deeply until no further move
  • Then backtrack and explore other branches
  • Continue until goal is found or all paths are explored
• Real-life examples:
  • File System Traversal: Opening folders inside folders (deep nesting). DFS goes till the last subfolder, then comes back. Used in file explorers (Windows, Mac, Linux)
  • Puzzle Solving (Sudoku, 8-Puzzle, etc.): DFS explores one possible solution path fully. If it doesn’t work, it backtracks. Useful in game trees or AI bots solving puzzles.
• Use Cases:
  • Topological Sorting
  • Cycle detection in graphs
  • Solving puzzles and mazes
  • Searching deep decision trees

---

BFS vs DFS

Aspect	BFS (Breadth First Search)	DFS (Depth First Search)
Traversal Order	Explores level by level (siblings before children).	Explores depth first (children before siblings).
Data Structure Used	Queue (FIFO).	Stack (LIFO) or recursion.
Path Finding	Finds the shortest path if it exists.	Does not guarantee shortest path.
Suitability	Best when the solution is closer to the source.	Best when the solution is far from the source.
Memory Usage	Requires more memory (stores all nodes at current level).	Requires less memory compared to BFS.
Node Visits	Each node is traversed only once.	Each node may be traversed twice due to backtracking.
Guarantee of Solution	Always finds a solution if one exists.	May get stuck in infinite loop and fail to find a solution.
Concept	FIFO – First In First Out.	LIFO – Last In First Out.
Real-life Examples	- Social media friend suggestion- Web crawlers- Google Maps shortest path	- File system traversal- Puzzle solving (Sudoku, 8-puzzle)- Game trees
Use Cases	- Shortest path in graphs- Web crawling- Social networks	- Topological sorting- Cycle detection- Maze/puzzle solving

---

Hill Climbing Algorithm

• Hill Climbing is an informed search algorithm (a type of greedy algorithm) used in Artificial Intelligence for optimization problems.

• The main goal is to reach the best possible solution by iteratively moving to better neighboring states until no further improvement is possible.

• Type: Informed Search (Greedy)

• Goal: Reach the peak (best solution) by always moving to a better state

• Strategy: Move in the direction where the heuristic/value function improves

Concept

Imagine climbing a hill in thick fog where you cannot see the entire landscape. You can only look at the immediate neighbors and decide the next step:

1. Start at some point (initial solution).
2. Check the neighboring solutions.
3. Move to the neighbor with the highest value (steepest ascent).
4. Repeat until no better neighbor exists.
5. Stop at the point where no further improvement is possible.

Important: Hill Climbing does not backtrack or remember past paths. It only moves forward toward better states.

How Hill Climbing Works

1. Start from an initial state.
2. Evaluate the neighboring states.
3. Move to the neighbor with a higher value.
4. Repeat until:
   • No better neighbor is found, or
   • A stopping criterion is met.

Key Features

• Advantages:
  • Simple and fast
  • Requires less memory
  • Works well when heuristic function is good
• Limitations (Problems faced):
  • Local Maxima: The algorithm may stop at a peak that is not the global maximum.
  • Plateau: The algorithm may get stuck in a flat region where all neighbors are of the same value.
  • Ridges: The algorithm may fail in narrow regions that require sideways movement before going upward.

Common Problems in Hill Climbing

1. Local Maximum
   • Definition: A point higher than its neighbors but lower than the global maximum.
   • Example: Climbing a small hill and assuming it is the highest point while a taller mountain exists nearby.
2. Plateau (Flat Maximum)
   • Definition: A flat area with no change in value in any direction.
   • Example: Reaching a flat surface on the hill where every step looks the same, leaving the algorithm “stuck.”
3. Ridge
   • Definition: A narrow path that requires sideways movement before going upward.
   • Example: The algorithm insists on moving straight up, missing the correct zigzag path.

Variants of Hill Climbing

• Simple Hill Climbing: Chooses the first better neighbor found.
• Steepest-Ascent Hill Climbing: Evaluates all neighbors and selects the steepest upward move.
• Stochastic Hill Climbing: Chooses randomly among the better neighbors to avoid being stuck.

Applications of Hill Climbing

• Artificial Intelligence in Games: For decision-making in games like Tic Tac Toe.
• Function Optimization: Finding maximum/minimum values of mathematical functions.
• Robotics and Pathfinding: To optimize paths or movement.
• Machine Learning Parameter Tuning: Adjusting parameters to improve performance.

Key Insight

• Hill Climbing is like climbing a mountain with a flashlight in fog:

  • You can only see a few steps ahead.
  • You always move upward if possible.
  • You stop when no better step is visible.

• Reference: https://www.scaler.com/topics/hill-climbing-in-ai/

---

Heuristic Search

• Heuristic Search is an informed search technique that uses additional knowledge (heuristics) to guide the search process towards the goal more efficiently.

• Type: Informed Search
• Heuristic: An educated guess or rule of thumb that helps estimate how close a state is to the goal.
• Goal: Reduce unnecessary exploration by selecting the most promising paths first.

Concept

• In heuristic search, instead of exploring all possible paths (as in uninformed search), the algorithm uses a heuristic function h(n) to estimate the cost or distance from a node n to the goal.

• Heuristic acts like a hint or shortcut.
• It does not always guarantee the optimal solution, but it often finds a good solution faster.
• The effectiveness of heuristic search depends heavily on the quality of the heuristic function.

How Heuristic Search Works

1. Start from the initial node.
2. Use the heuristic function h(n) to evaluate which node seems closer to the goal.
3. Select the most promising node.
4. Expand the chosen node and repeat the evaluation for its successors.
5. Continue until the goal node is reached.

Real-Life Analogies

1. Treasure Hunt Analogy

   • Instead of checking every possible place, you use hints (“warmer/colder”) to guess where the treasure might be.

2. Candy Search at Home

   • You want to find candy but instead of checking every location (drawers, fridge, shoe rack…), you use your intuition:
     • “Maybe in the fridge?” (likely)
     • “Under the bed?” (unlikely)

3. Navigation Apps (Google Maps)

   • Example: Traveling from Srinagar to Pahalgam.
   • Google suggests the route based not only on distance but also on estimated time.
   • This estimation = heuristic in action.

Example: Search Tree with Heuristics

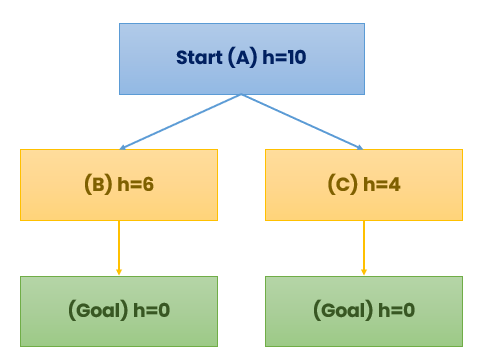
• Both B and C lead to the goal, but the heuristic indicates C looks closer (h=4 < h=6).
• The algorithm selects C first and reaches the goal faster.

Key Features

• Advantages:

  • Faster than uninformed searches like BFS and DFS.
  • Can skip irrelevant or bad branches.
  • Requires less memory and computation if heuristics are good.

• Disadvantages:

  • Heuristic must be accurate and admissible (should not overestimate cost).
  • Poor heuristics may lead to misleading paths or incorrect solutions.
  • Designing good heuristics is often challenging.

Applications of Heuristic Search

• Navigation systems: Google Maps, Uber routes
• Game AI: Chess, Tic Tac Toe
• Puzzle solving: 8-Puzzle, Sudoku
• Decision-making: Intelligent agents, smart bots

Key Insight

• Heuristic Search is like searching with a guide: instead of blindly exploring every possibility, you follow hints (heuristics) that lead you towards the goal faster.

• Reference: https://www.scaler.com/topics/artificial-intelligence-tutorial/informed-search/#heuristics-function

---